凌云的博客

LeetCode 算法题 3. 无重复字符的最长子串

分类：algorithm| 发布时间：2016-06-24 12:30:00

---

题目

给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

思路

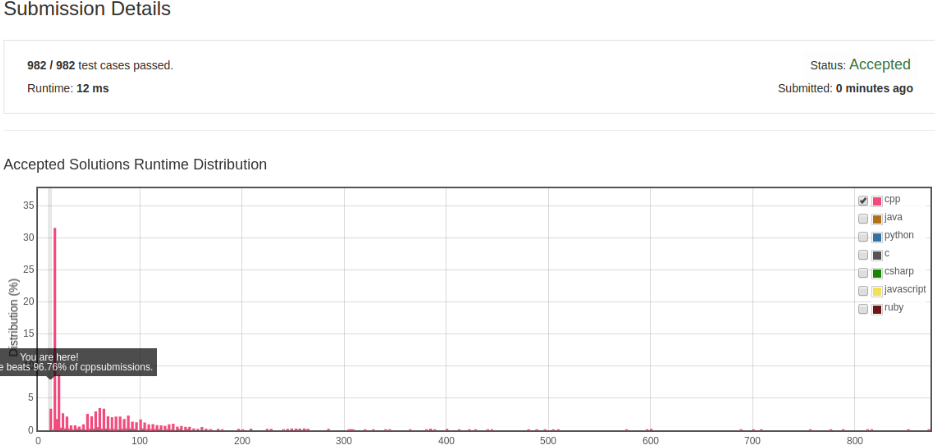
最直观的方法当然就是暴力搜索了，用一个 bool 类型的数组记录某个字符是否出现过， 两层循环搜索给出的字符串，外层循环给出搜索的起点，内层循环检查当前字符是否已经出现过。 这种方法的复杂度为 O(n^2)。

换个思路，将记录字符是否出现过的数组改为 int 类型，-1 表示未出现，否则就是出现过， 其值就是所在的下标。 遍历给出的数组，用当前字符（c）查询 table[c] 的值，若为 -1 则将当前长度增加为 1， 并将当前下标记录到 table[c] 中。 否则将当前长度重置为 i - table[c] （i 为当期下标）并将之前长度到当前长度之间的 table 的值设置为 -1。

for (int j = i - count; j < curIdx; ++j) {
    table[s[j]] = -1;
}

count = i - table[c];

C++ 算法实现

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int table[256];
        fill(table, table + 256, -1);
        int curIdx = 0;
        int count = 0;
        int maxCount = 0;
        const int size = s.size();
        for (int i = 0; i != size; ++i) {
            curIdx = table[s[i]];
            if (-1 == curIdx) {
                ++count;
                maxCount = max(count, maxCount);
            } else {
                for (int j = i - count; j < curIdx; ++j) {
                    table[s[j]] = -1;
                }

                count = i - curIdx;
            }

            table[s[i]] = i;
        }

        return maxCount;
    }
};

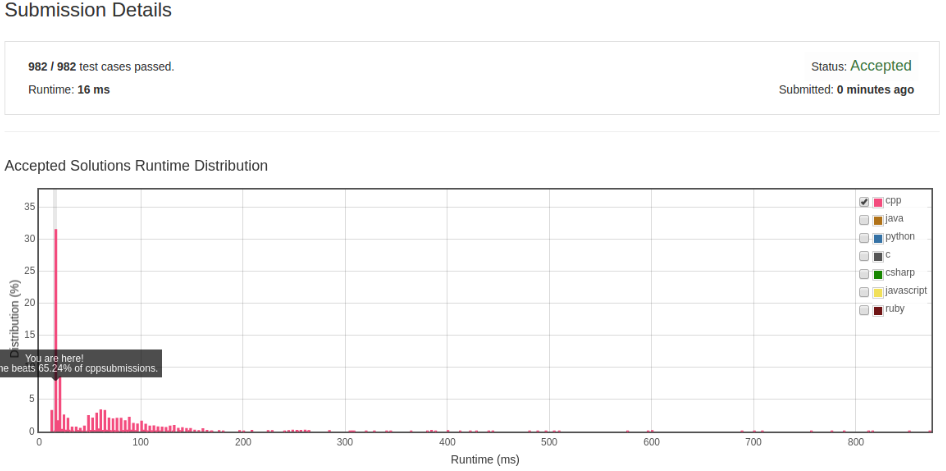
更进一步

在上个算法中当 table[c] 不为 -1 时 执行：

for (int j = i - count; j < curIdx; ++j) {
    table[s[j]] = -1;
}

count = i - table[c];

是不必要的，其实只要记录上一个不重复字符的下标，当 curIdx 大于等于不重复下标时， 重新设置不重复的下标。

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int table[256];
        fill(table, table + 256, -1);
        int maxCount = 0;
        int noDupStart = 0;
        const int size = s.size();
        for (int i = 0; i != size; ++i) {
            int current = s[i];
            int curIdx = table[current];
            if (curIdx >= noDupStart) {
                maxCount = max(maxCount, i - noDupStart);
                noDupStart = curIdx + 1;
            }

            table[current] = i;
        }

        return max(maxCount, int(s.size()) - noDupStart);
    }
};