LeetCode 算法题 37. 解数独

分类：algorithm| 发布时间：2016-09-29 18:45:00

题目

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 '.' 表示。

一个数独。

答案被标成红色。

注意：

给定的数独序列只包含数字 1-9 和字符 '.' 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

解法 1

可以通过 DFS 算法得到。

class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        dfs(board, 0);
    }

    bool dfs(vector<vector<char>>& board, const int pos) {
        if (pos == 81) {
            return true;
        }

        int x = pos / 9, y = pos % 9;
        if (board[x][y] != '.') {
            return dfs(board, pos + 1);
        }

        for (char i = '0'; i <= '9'; ++i) {
            board[x][y] = i;
            if (isValidSudoku(board) && dfs(board, pos + 1))
                return true;
        }

        board[x][y] = '.';
        return false;
    }

    bool isValidSudoku(vector<vector<char>>& board) {
        int col[9][9] = {0}, row[9][9] = {0}, rec[9][9] = {0};
        for(int i = 0; i < 9; ++ i) {
            for(int j = 0; j < 9; ++ j) {
                if(board[i][j] != '.') {
                    int num = board[i][j] - '0' - 1, k = i / 3 * 3 + j / 3;
                    if(col[i][num] || row[j][num] || rec[k][num])
                        return false;

                    col[i][num] = row[j][num] = rec[k][num] = 1;
                }
            }
        }

        return true;
    }
};

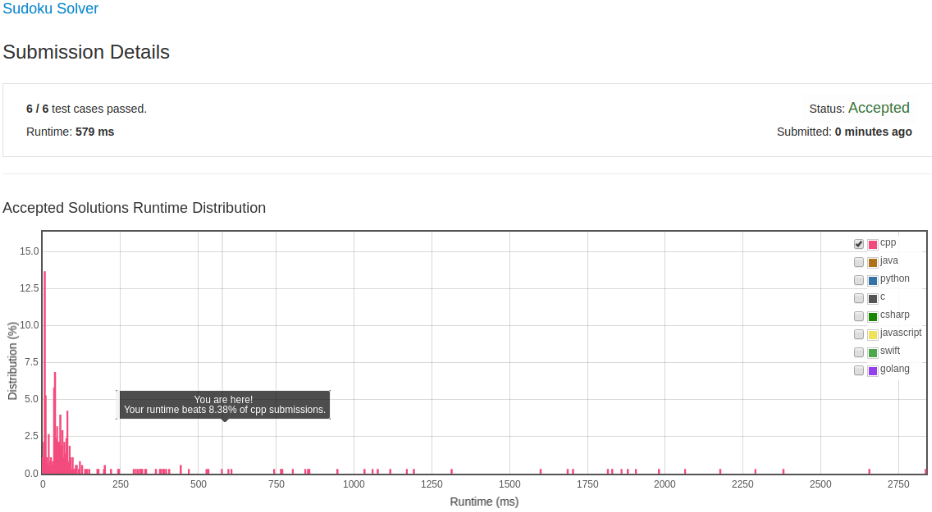
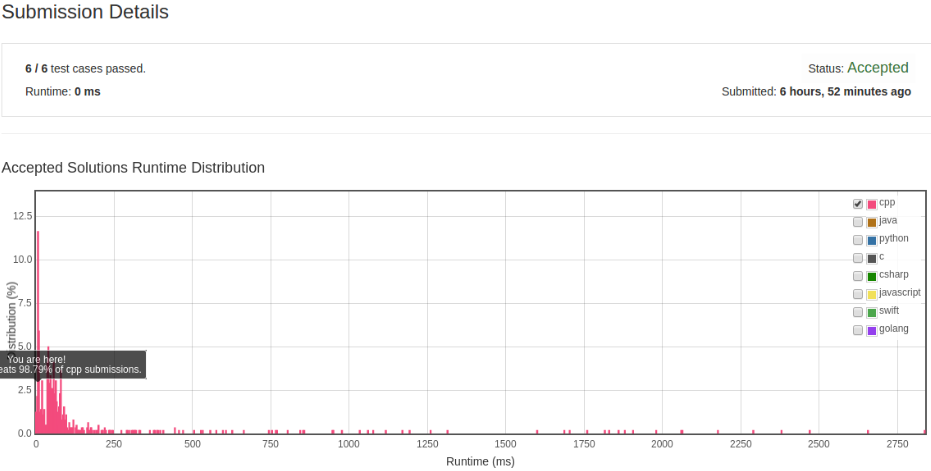
这个算法应该比较好理解，同时还用到了上一题的函数来判断解是否合法。但是效率就比较差了，其实不用每次都检查整个数独是否合法，只用检查当前的行列以及区块就行了。

class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        dfs(board, 0);
    }

    bool dfs(vector<vector<char>>& board, const int pos) {
        if (pos == 81)
            return true;

        int x = pos / 9, y = pos % 9;
        if (board[x][y] != '.')
            return dfs(board, pos + 1);

        for (char i = '0'; i <= '9'; ++i) {
            board[x][y] = i;
            if (check(board, x, y) && dfs(board, pos + 1))
                return true;
        }

        board[x][y] = '.';
        return false;
    }

    bool check(vector<vector<char>>& board, int x, int y) {
        int col[9] = {0}, row[9] = {0}, rec[9] = {0};
        const int start_x = (x / 3) * 3, start_y = (y / 3) * 3;
        for(int i = 0; i < 9; ++ i) {
            if(board[x][i] != '.') {
                int num = board[x][i] - '0' - 1;
                if (col[num]) {
                    return false;
                }

                col[num] = 1;
            }

            if (board[i][y] != '.') {
                int num = board[i][y] - '0' - 1;
                if (row[num]) {
                    return false;
                }

                row[num] = 1;
            }

            int delta_x = i % 3, delta_y = i / 3;
            if (board[start_x + delta_x][start_y + delta_y] != '.') {
                int num = board[start_x + delta_x][start_y + delta_y] - '0' - 1;
                if (rec[num]) {
                    return false;
                }

                rec[num] = 1;
            }
        }

        return true;
    }
};

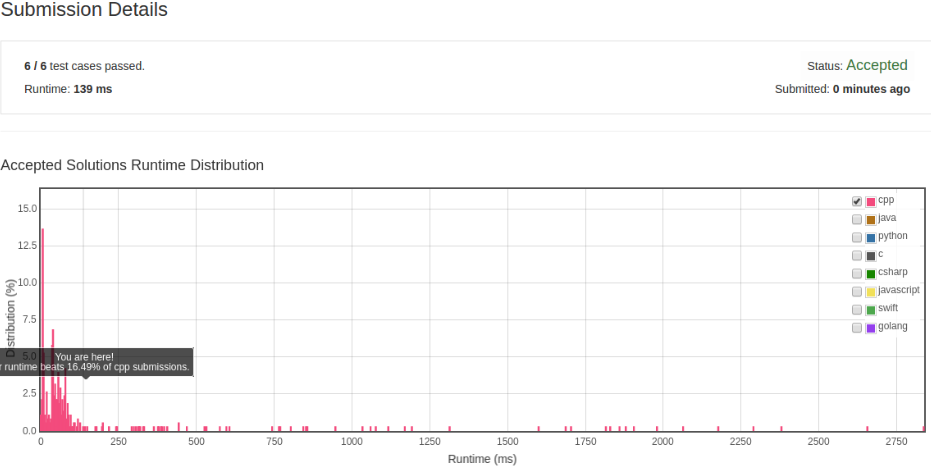
可以看到修改后的版本有了较大的提升。其实我们可以更进一步，给定一个坐标，得到该坐标上合法的值。

class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        dfs(board, 0);
    }

    bool dfs(vector<vector<char>>& board, const int pos) {
        if (pos == 81) {
            return true;
        }

        int x = pos / 9, y = pos % 9;
        if (board[x][y] != '.') {
            return dfs(board, pos + 1);
        }

        int invalidNums[9] = {0};
        getInvalidNums(board, x, y, invalidNums);
        for (int i = 0; i < 9; ++i) {
            if (invalidNums[i]) continue;
            board[x][y] = i + '1';
            if (dfs(board, pos+1)) {
                return true;
            }
        }

        board[x][y] = '.';
        return false;
    }

    void getValidNums(vector<vector<char>>& board, int x, int y, int *nums) {
        const int start_x = (x / 3) * 3, start_y = (y / 3) * 3;
        for(int i = 0; i < 9; ++ i) {
            if(board[x][i] != '.') {
                int num = board[x][i] - '0' - 1;
                nums[num] = 1;
            }

            if (board[i][y] != '.') {
                nt num = board[i][y] - '0' - 1;
                nums[num] = 1;
            }

            int new_x = start_x + i % 3, new_y = start_y + i / 3;
            if (board[new_x][new_y] != '.') {
                int num = board[new_x][new_y] - '0' - 1;
                nums[num] = 1;
            }
        }
    }
};

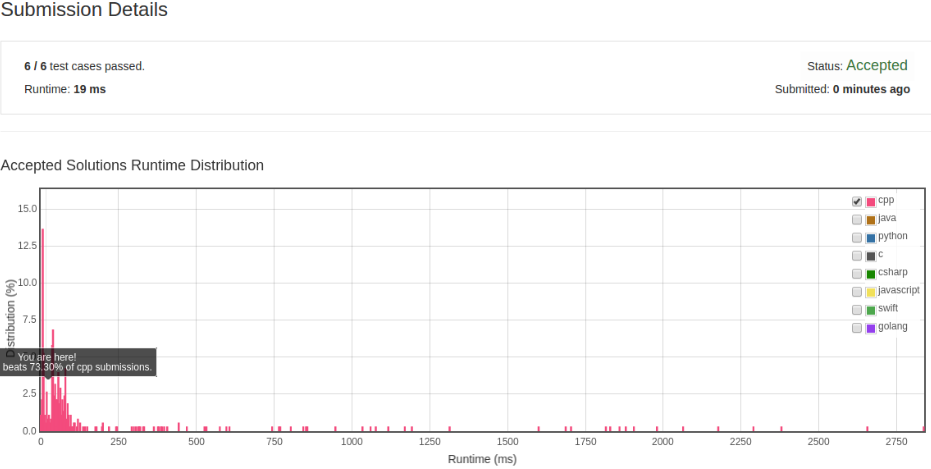
通过直接获取指定坐标的合法的值可以免除每次检查某个值在特定点上是否合法的操作，大大减少了相关的时间。可以看到这个版本相比上一个版本效率已经不在一个数量级上了。那么这个算法是否可以再进一步呢？在这个算法中每次调用 dfs(...) 函数都需要获取合法的数字，其实这个操作也是可以去掉了。具体方法是一开始就根据 board 来生成每一行每一列以及每一块的合法值，而不用每次调用 dfs(...) 都生成，减少可能出现的重复。

class Solution {
public:
    void solveSudoku(vector<vector<char>>& board) {
        memset(col, 0, sizeof(col));
        memset(row, 0, sizeof(row));
        memset(rec, 0, sizeof(rec));
        for(int i = 0; i < 9; i++) {
            for(int j = 0; j < 9; j++) {
                if(board[i][j] == '.') continue;
                int temp = 3 * (i / 3) + j / 3;
                int num = board[i][j] - '1';
                col[j][num] = row[i][num] = rec[temp][num] = 1;
            }
        }

        dfs(board, 0);
    }

    bool dfs(vector<vector<char>>& board, const int pos) {
        if (pos == 81) {
            return true;
        }

        const int x = pos / 9, y = pos % 9;
        if (board[x][y] != '.') {
            return dfs(board, pos + 1);
        }

        int temp = 3 * (x / 3) + y / 3;
        for (char i = 0; i < 9; ++i) {
            if (col[y][i] || row[x][i] || rec[temp][i]) {
                continue;
            }

            col[y][i] = row[x][i] = rec[temp][i] = 1;
            if (dfs(board, pos + 1)) {
                board[x][y] = i + '1';
                return true;
            }

            col[y][i] = row[x][i] = rec[temp][i] = 0;
        }

        return false;
    }

private:
    int col[9][9];
    int row[9][9];
    int rec[9][9];
};

解法 2

这个方法是这里分享的：Sharing my 2ms C++ solution with comments and explanations

这个解法和我们解法 1 的最后一个方案类似，只是他会先将每个空格子按照有可能的数字个数按从少到多进行排序，然后再进行尝试。进一步减少尝试的次数。

class Solution {
    struct cell { // encapsulates a single cell on a Sudoku board
        uint8_t value; // cell value 1..9 or 0 if unset
        uint8_t numPossibilities; // number of possible (unconstrained) values for the cell
        bitset<10> constraints; // if bitset[v] is 1 then value can't be v
        cell() : value(0), numPossibilities(9),constraints() {};
    };

    array<array<cell,9>,9> cells;

    // sets the value of the cell to [v]
    // the function also propagates constraints to other cells and deduce new values where possible
    bool set(int i, int j, int v) {
        // updating state of the cell
        cell& c = cells[i][j];
        if (c.value == v)
            return true;

        if (c.constraints[v])
            return false;

        c.constraints = bitset<10>(0x3FE); // all 1s
        c.constraints.reset(v);
        c.numPossibilities = 1;
        c.value = v;

        // propagating constraints
        for (int k = 0; k<9; k++) {
            // to the row:
            if (i != k && !updateConstraints(k, j, v))
                return false;

            // to the column:
            if (j != k && !updateConstraints(i, k, v))
                return false;

            // to the 3x3 square:
            int ix = (i / 3) * 3 + k / 3;
            int jx = (j / 3) * 3 + k % 3;
            if (ix != i && jx != j && !updateConstraints(ix, jx, v))
                return false;
        }

        return true;
    }

    // update constraints of the cell i,j by excluding possibility of 'excludedValue'
    // once there's one possibility left the function recurses back into set()
    bool updateConstraints(int i, int j, int excludedValue) {
        cell& c = cells[i][j];
        if (c.constraints[excludedValue])
            return true;

        if (c.value == excludedValue)
            return false;

        c.constraints.set(excludedValue);
        if (c.value || --c.numPossibilities > 1)
            return true;

        for (int v = 1; v <= 9; v++) {
            if (!c.constraints[v]) {
                return set(i, j, v);
            }
        }

        return false;
    }

    // backtracking state - list of empty cells
    vector<pair<int, int>> bt;

    // find values for empty cells
    bool findValuesForEmptyCells() {
        // collecting all empty cells
        bt.clear();
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (!cells[i][j].value)
                    bt.push_back(make_pair(i, j));
            }
        }

        // making backtracking efficient by pre-sorting empty cells by numPossibilities
        sort(bt.begin(), bt.end(), [this](const pair<int, int>&a, const pair<int, int>&b) {
                return cells[a.first][a.second].numPossibilities < cells[b.first][b.second].numPossibilities; });
        return backtrack(0);
    }

    // Finds value for all empty cells with index >=k
    bool backtrack(int k) {
        if (k >= bt.size())
            return true;

        int i = bt[k].first;
        int j = bt[k].second;
        // fast path - only 1 possibility
        if (cells[i][j].value)
            return backtrack(k + 1);

        auto constraints = cells[i][j].constraints;
        // slow path >1 possibility.
        // making snapshot of the state
        array<array<cell,9>,9> snapshot(cells);
        for (int v = 1; v <= 9; v++) {
            if (!constraints[v]) {
                if (set(i, j, v)) {
                    if (backtrack(k + 1))
                        return true;
                }

                // restoring from snapshot,
                // note: computationally this is cheaper
                // than alternative implementation with undoing the changes
                cells = snapshot;
            }
        }

        return false;
    }

public:
    void solveSudoku(vector<vector<char>> &board) {
        cells = array<array<cell,9>,9>(); // clear array
        // Decoding input board into the internal cell matrix.
        // As we do it - constraints are propagated and even additional values are set as we go
        // (in the case if it is possible to unambiguously deduce them).
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] != '.' && !set(i, j, board[i][j] - '0'))
                    return; // sudoku is either incorrect or unsolvable
            }
        }

        // if we're lucky we've already got a solution,
        // however, if we have empty cells we need to use backtracking to fill them
        if (!findValuesForEmptyCells())
            return; // sudoku is unsolvable

        // copying the solution back to the board
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (cells[i][j].value)
                    board[i][j] = cells[i][j].value + '0';
            }
        }
    }
};

凌云的博客

行胜于言