凌云的博客

LeetCode 算法题 9. 回文数

分类：algorithm| 发布时间：2016-06-28 09:41:00

---

题目

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

示例 1:

输入: 121
输出: true

示例 2:

输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

示例 3:

输入: 10
输出: false
解释: 从右向左读, 为 01 。因此它不是一个回文数。

进阶:

你能不将整数转为字符串来解决这个问题吗？

解法 1

class Solution {
public:
    bool isPalindrome(int x) {
        if (x < 0) {
            return false;
        }

        // equivalence pow(10, log10(x))
        int p = 1;
        while (x / p >= 10) {
            p *= 10;
        }

        while (x) {
            if (x / p != x % 10) {
                return false;
            }

            x -= (x % 10) * p;
            x /= 10;
            p /= 100;
        }

        return true;
    }
};

依照定义逐次对比最高位和最低位的数字。

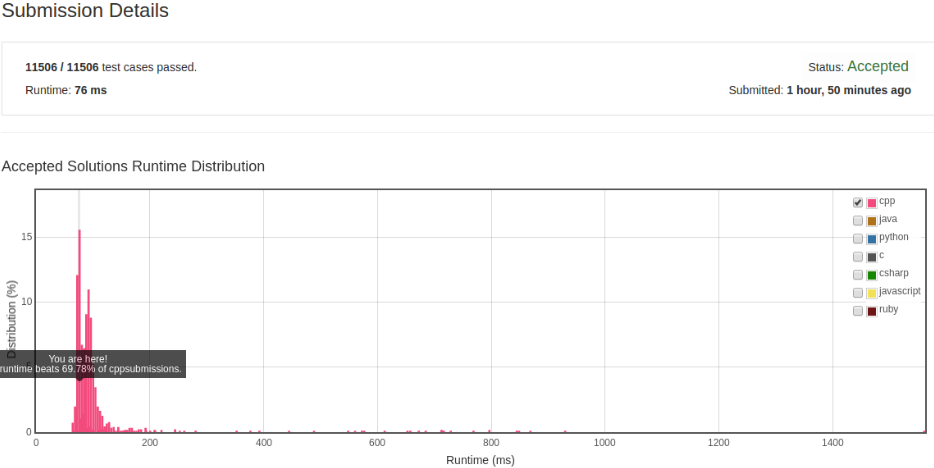
解法 2

class Solution {
public:
    bool isPalindrome(int x) {
        if(x < 0) return false;
        int revhalf = 0, slow = x, fast = x;
        while (fast) {
            revhalf = revhalf * 10 + slow % 10;
            slow /= 10;
            fast /= 100;
        }

        return slow == revhalf || slow == revhalf / 10;
    }
};

翻转数字的一半然后对比。

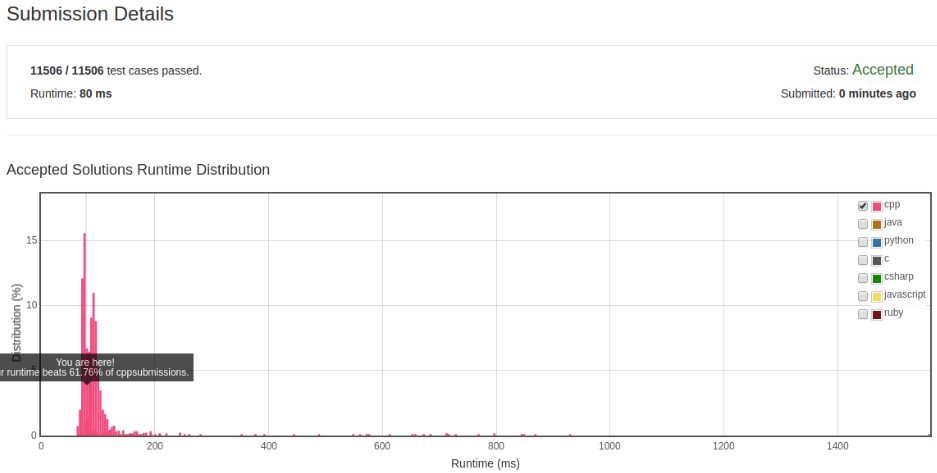
解法 3

class Solution {
public:
    bool isPalindrome(int x) {
        if (x < 0) return false;
        long mirror = 0;
        int cache = x;
        while (x) {
            mirror = mirror * 10 + x % 10;
            x /= 10;
        }

        return mirror == cache;
    }
};

翻转数字然后对比。

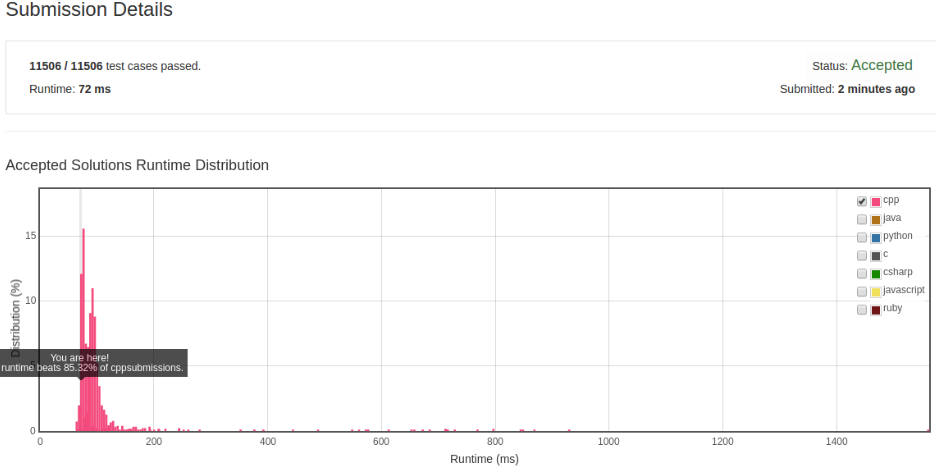
解法 4

class Solution {
public:
    bool isPd(int &xd, int xn) {
        if (xn / 10 == 0) {
            return (xd % 10) == xn;
        } else {
            return isPd(xd, xn/10) && (xn % 10) == (xd=xd/10) % 10;
        }
    }

    bool isPalindrome(int x) {
        if (x < 0) return false;
        return isPd(x, x);
    }
};