凌云的博客

LeetCode 算法题 11. 盛最多水的容器

分类：algorithm| 发布时间：2016-07-01 08:11:00

---

题目

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。 在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。 找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

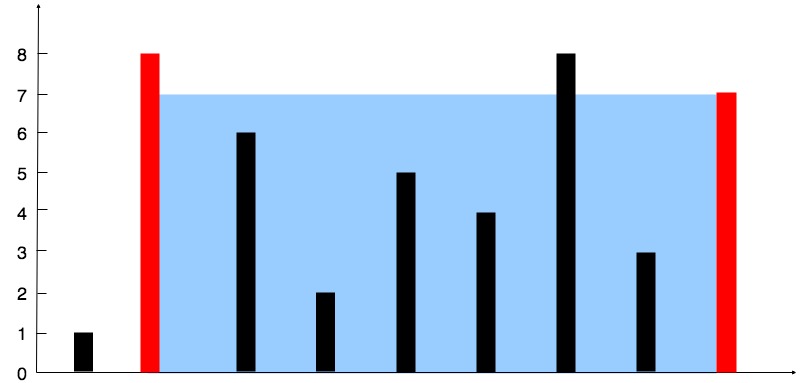
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。 在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

解法

影响容器的容量的因素有两个，一个是 i 与 j 之间的距离，距离越大越好， 一个是 min(ai, aj) 这个值也是越大越好。 先给出解法：

class Solution {
public:
    int maxArea(vector<int>& height) {
        const int size = height.size();
        int maxArea = 0;
        for (int i = 0, j = size - 1; i != j; ) {
            if (height[i] >= height[j]) {
                maxArea = max(maxArea, (j - i) * (height[j]));
                --j;
            } else {
                maxArea = max(maxArea, (j - i) * (height[i]));
                ++i;
            }
        }

        return maxArea;
    }
};

为什么这种解法是对的呢，假设我们有个长度为 6 的数组， 那么要解出最大值的直接方法是算法任意两个距离的大小， 然后取其最大值。 由于 i 和 j 不能取同样的值，因此 i 和 j 相同的情况不用算，我们用 'x' 来标记。

    1 2 3 4 5 6
  1 x
  2 x x
  3 x x x
  4 x x x x
  5 x x x x x
  6 x x x x x x

假设 i 为行号，j 为列号。 我们首先计算 i 和 j 最大的情况，我们用 'o' 标记算出的结果，假设 a6 大于 a1。 那么 (1, a1) 和 (6, a6) 的结果等于 (6 - 1) * a1。 同时 a1 和 a2..a5 的面积都不用算了，因为肯定比 a1 也 a6 的面积小。 首先是长度 (j - i) 肯定是变小的，其次是高度肯定是不比 a1 高。 我们用 '-' 或 '|' 来标记不用算的情况：

    1 2 3 4 5 6
  1 x - - - - o
  2 x x
  3 x x x
  4 x x x x
  5 x x x x x
  6 x x x x x x

将 i 往前移动，对比 a2 和 a6 的大小，如果是 a2 比 a6 小，情况与上一步一样。 我们这里假设 a2 比 a6 大。 相似地由于 a6 < a2，因此 a6 与 a3..a5 的面积肯定比 a2 与 a6 的面积小。

    1 2 3 4 5 6
  1 x ------- o
  2 x x       o
  3 x x x     |
  4 x x x x   |
  5 x x x x x |
  6 x x x x x x

然后将 j 减 1,对比 a2 和 a5 的大小。 通过这样的方法，我们只用算出尽量少的情况（也就是标记为 ‘o' 的情况）。 然后取其最大值就是解。这个算法的复杂度为 O(n)。