凌云的博客

LeetCode 算法题 28. 实现 strStr()

分类：algorithm| 发布时间：2016-08-04 23:23:00

---

题目

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。 如果不存在，则返回  -1。

示例 1:

输入: haystack = "hello", needle = "ll"
输出: 2

示例 2:

输入: haystack = "aaaaa", needle = "bba"
输出: -1

说明:

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

暴力查找

class Solution {
public:
    int strStr(string haystack, string needle) {
        const int size = haystack.size();
        const int nsize = needle.size();

        for (int i = 0; i <= size - nsize; ++i) {
            if (!strncmp(haystack.c_str() + i, needle.c_str(), nsize)) {
                return i;
            }
        }

        return -1;
    }
};

这个算法的最坏情况为 MN 一般情况为 1.1N，其中 M 为模式串的长度，N 为文本串的长度。

Knuth-Morris-Pratt 算法（KMP）

KMP 算法的重点是根据模式串构造出一个 next 表，当比较失败时不对 i （文本串的指针）进行回退，而是根据 next 表对 j （模式串的指针）进行设置。

class Solution {
public:
    int strStr(string haystack, string needle) {
        int M = needle.length(), N = haystack.length();
        if (M == 0) {
            return 0;
        }

        int next[M]{0};
        for(int i = 1; i < M; ++i) {
            int j = next[i-1];
            while(j>0 && needle[i] != needle[j]) {
                j = next[j-1];
            }

            next[i] += j + (needle[i] == needle[j]); //the length of the matched prefix;
        }

        int i = 0, j = 0;
        while(i < N) {
            if (haystack[i] == needle[j]) {
                ++i;
                ++j;
                if (j == M) return i - j;
            } else if (j > 0) {
                j = next[j-1];
            } else {
                ++i;
            }
        }

        return -1;
    }
};

这个算法的最坏情况为 3N，一般情况为 1.1N。 关于这个算法的更详细说明可以参考：

• WIKI: Knuth–Morris–Pratt_algorithm
• The Knuth-Morris-Pratt Algorithm in my own words

Boyer-Moore 算法

BM 的特点是从模式串的后面开始匹配，当匹配失败时通过两个并行的策略尽量大的移动 i。

坏字符算法

当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对，然后继续匹配。 坏字符算法有两种情况。

• Case1：模式串中有对应的坏字符时，让模式串中最靠右的对应字符与坏字符相对（PS：BM 不可能走回头路，因为若是回头路，则移动距离就是负数了，肯定不是最大移动步数了），如下图。
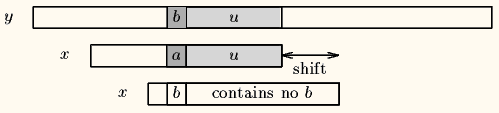
• Case2：模式串中不存在坏字符，很好，直接将 i 移到 j + 1的地方，如下图。

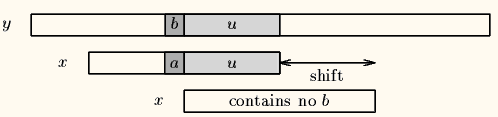
BM 算法的任意一个策略都可以作为一个独立的算法来用，比如可以只实行坏字符算法：

class Solution {
public:
    int strStr(string haystack, string needle) {
        if (needle.empty()) return 0;
        if (haystack.empty()) return -1;

        int N = haystack.size();
        int M = needle.size();
        int R = 256;
        int bc[R]{-1};
        buildBC(bc, needle, M);

        int skip = 0;
        for (int i = 0; i <= N - M; i += skip) {
            int j = M - 1;
            for (; j >= 0 && needle[j] == haystack[i + j]; --j) ;
            if (j < 0) return i;
            skip = max(1, j - bc[haystack[i + j]]);
        }

        return -1;
    }

    void buildBC(int bc[], const string &needle, int M) {
        for (int i = 0; i < M; ++i) {
            bc[needle[i]] = i;
        }
    }
};

好后缀算法

如果程序匹配了一个好后缀, 并且在模式中还有另外一个相同的后缀或后缀的部分, 那把下一个后缀或部分移动到当前后缀位置。 假如说，pattern 的后 u 个字符和 text 都已经匹配了，但是接下来的一个字符不匹配，我需要移动才能匹配。

如果说后 u 个字符在 pattern 其他位置也出现过或部分出现，我们将 pattern 右移到前面的 u 个字符或部分和 最后的 u 个字符或部分相同，如果说后 u 个字符在 pattern 其他位置完全没有出现，很好，直接右移整个 pattern。

这样，好后缀算法有三种情况，如下图所示：

• Case1：模式串中有子串和好后缀完全匹配，则将最靠右的那个子串移动到好后缀的位置继续进行匹配。
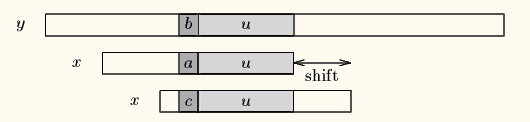
• Case2：如果不存在和好后缀完全匹配的子串，则在好后缀中找到具有如下特征的最长子串, 使得 P[m-s…m]=P[0…s]。
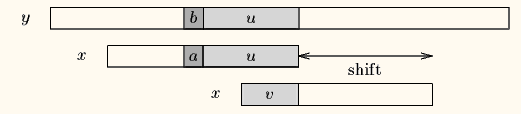
• Case3：如果完全不存在和好后缀匹配的子串，则右移整个模式串。

计算好后缀数组 bmGs[]

bmGs[] 的下标是数字而不是字符，表示字符在 pattern 中位置。

如前所述，bmGs 数组的计算分三种情况，与前一一对应。 假设图中好后缀长度用数组 suff[] 表示。

• Case1：对应好后缀算法 case1，如下图，j 是好后缀之前的那个位置。
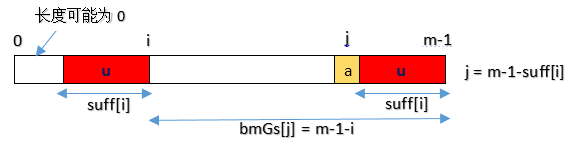
• Case2：对应好后缀算法 case2：如下图所示：
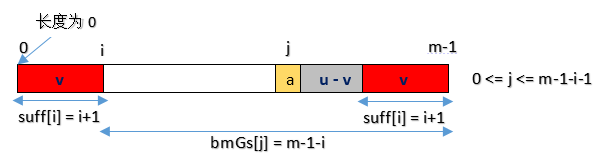
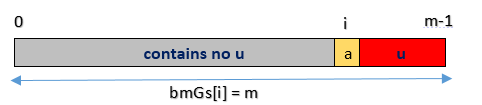
• Case3：对应好后缀算法 case3，bmGs[i] = strlen（pattern）= m

void buildGS(int gs[], const string &needle, int m) {
    int i, j;

    int suff[m];
    suffix(needle.c_str(), m, suff);

    // Case3
    for (i = 0; i < m; i++) {
        gs[i] = m;
    }

    // Case2
    for (i = 0; i < m; ++i) {
        if(suff[i] == i + 1) {
            for(int j = 0; j < m - 1 - i; j++) {
                if(gs[j] == m)
                    gs[j] = m - 1 - i;
            }
        }
    }

    // Case1
    for (i = 0; i <= m - 2; i++) {
        gs[m - 1 - suff[i]] = m - 1 - i;
    }
}

接下来是 suff 数组，这个数组怎么得到呢？ 先看看这个数组的定义：suff[i] 就是求 pattern 中以 i 位置字符为后缀和以最后一个字符为后缀的公共后缀串的长度。

因此 suff 可以这样得到：

void suffix(char *pattern, int m, int suff[])
{
    int i, j;
    int k;

    suff[m - 1] = m;
    for(i = m - 2; i >= 0; i--) {
        j = i;
        while(j >= 0 && pattern[j] == pattern[m - 1 - (i - j)]) j--;
        suff[i] = i - j;
    }
}

这样可能就万事大吉了，可是总有人对这个算法不满意，感觉太暴力了， 于是有聪明人想出一种方法，对上述常规方法进行改进。 基本的扫描都是从右向左，改进的地方就是利用了已经计算得到的 suff[] 值， 计算现在正在计算的suff[]值。

具体怎么利用，看下图：

i 是当前正准备计算 suff[] 值的那个位置。

f 是上一个成功进行匹配的起始位置 （不是每个位置都能进行成功匹配的， 实际上能够进行成功匹配的位置并不多）。

g 是上一次进行成功匹配的失配位置。

如果 i 在 g 和 f 之间，那么一定有 P[i]=P[m-1-f+i]；并且如果 suff[m-1-f+i] < i-g, 则 suff[i] = suff[m-1-f+i]，这不就利用了前面的suff了吗。

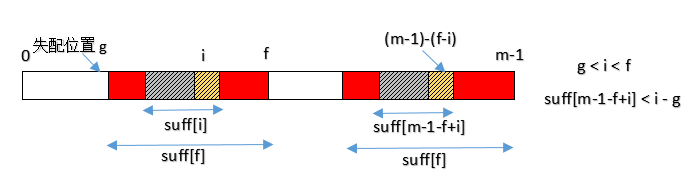
好了，这样解释过后，代码也比较简单：

void suffix(const char *pattern, int m, int suff[]) {
    int f, g, i;

    suff[m - 1] = m;
    g = m - 1;
    for (i = m - 2; i >= 0; --i) {
        if (i > g && suff[i + m - 1 - f] < i - g) {
            suff[i] = suff[i + m - 1 - f];
        } else {
            if (i < g) g = i;
            f = i;

            while (g >= 0 && pattern[g] == pattern[g + m - 1 - f]) --g;
            suff[i] = f - g;
        }
    }
}

整体实现

将上述代码整合起来，就得到了完整的 BM 算法。

class Solution {
public:
    int strStr(string haystack, string needle) {
        if (needle.empty()) return 0;
        if (haystack.empty()) return -1;

        int N = haystack.size();
        int M = needle.size();
        int R = 256;
        int bc[R]{-1};
        buildBC(bc, needle, M);
        int gs[M];
        buildGS(gs, needle, M);

        int skip = 0;
        for (int i = 0; i <= N - M; i += skip) {
            int j = M - 1;
            for (; j >= 0 && needle[j] == haystack[i + j]; --j) ;
            if (j < 0) return i;
            skip = max(gs[j], j - bc[haystack[i + j]]);
        }

        return -1;
    }

    void buildBC(int bc[], const string &needle, int m) {
        for (int i = 0; i < m; ++i) {
            bc[needle[i]] = i;
        }
    }

    void buildGS(int gs[], const string &needle, int m) {
        int i, j;
        int suff[m];
        suffix(needle.c_str(), m, suff);

        // Case3
        for (i = 0; i < m; i++) {
            gs[i] = m;
        }

        // Case2
        for (i = 0; i < m; ++i) {
            if(suff[i] == i + 1) {
                for(int j = 0; j < m - 1 - i; j++) {
                    if(gs[j] == m)
                        gs[j] = m - 1 - i;
                }
            }
        }

        // Case1
        for (i = 0; i <= m - 2; i++) {
            gs[m - 1 - suff[i]] = m - 1 - i;
        }
    }

    void suffix(const char *pattern, int m, int suff[]) {
        int f, g, i;
        suff[m - 1] = m;
        g = m - 1;
        for (i = m - 2; i >= 0; --i) {
            if (i > g && suff[i + m - 1 - f] < i - g) {
                suff[i] = suff[i + m - 1 - f];
            } else {
                if (i < g) g = i;
                f = i;
                while (g >= 0 && pattern[g] == pattern[g + m - 1 - f]) --g;
                suff[i] = f - g;
            }
        }
    }
};

这个算法的最坏情况为 MN，一般情况为 N/M。

参考：

• WIKI: Boyer–Moore string search algorithm
• grep之字符串搜索算法Boyer-Moore由浅入深（比KMP快3-5倍）