LeetCode 算法题 31. 下一个排列

分类：algorithm| 发布时间：2016-09-22 10:59:00

题目

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。

1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

解法

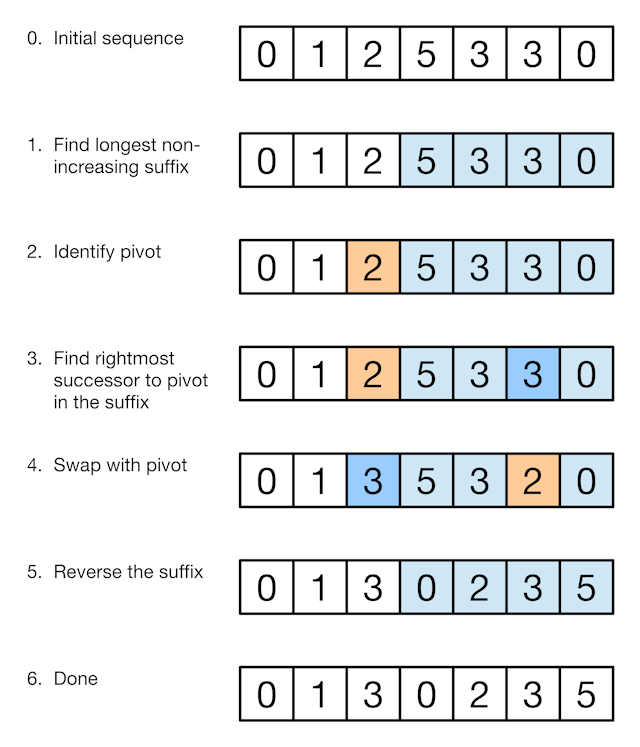
我们使用数组 (0, 1, 2, 5, 3, 3, 0) 作为例子。

关键点在于，要求出下一个排列就要尽可能少地增加这个数组。我们应该尽量修改靠右的数字，保持左边的数组不变。比如，相比将第一个数字由 0 改为 1,将 (0, 1) 修改为 (0, 2) 更接近下一个排列。当然，在这个例子中下一个排列不需要修改第二个数字。

首先，找出一个不能再增加的后缀。在我们的例子中，这个后缀为 (5, 3, 3, 0)。这个后缀已经是最高的排列了，所以我们不能只通过修改这个后缀来求出下一个排列——我们需要同时修改这个后缀左边的一个数字。

然后，将后缀左边的数字称为轴。（如果没有这么一个数字，那么这个序列已经是最后一个排列方式。）轴比后缀数组的第一个数字要小。因此后缀数组中至少有一个数字比轴要大。如果我们将轴与后缀数组中比轴大的数字中的最小的一个交换，那么前缀数组就是最小的增加了。（前缀数组为除后缀数组外的其他数字）在本例中，我们得到了前缀数组 (0, 1, 3) 以及后缀数组 (5, 3, ,2, 0)

最后，将后缀数组按从小到大排序，因为我们增加了前缀数组，因此我们需要将后缀数组变得尽可能小。其实我们可以反转后缀数组而不用将其排序，因为后缀数组本来就是按照从大到小排列的。因此我们得到了下一个排列： (0, 1, 3, 0, 2, 3, 5)

用数学方法描述就是：

找到最大的下标 i 使得 array[i - 1] < array[i]
找到最大的下标 j 使得 j > i 并且 array[j] > array[i - 1]
交换 array[j] 和 array[i - 1]
反转 i 开始的后缀数组

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        if (nums.empty()) return;

        // in reverse order, find the first number which is in increasing trend (we call it violated number here)
        int i;
        for (i = nums.size() - 2; i >= 0; --i) {
            if (nums[i] < nums[i+1]) break;
        }

        // reverse all the numbers after violated number
        reverse(begin(nums)+i+1, end(nums));
        // if violated number not found, because we have reversed the whole array, then we are done!
        if (i == -1) return;
        // else binary search find the first number larger than the violated number
        auto itr = upper_bound(begin(nums)+i+1, end(nums), nums[i]);
        // swap them, done!
        swap(nums[i], *itr);
    }
};

凌云的博客

行胜于言

LeetCode 算法题 31. 下一个排列

题目

解法

参考