凌云的博客

LeetCode 算法题 52. N皇后 II

分类：algorithm| 发布时间：2016-10-15 15:11:00

---

题目

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

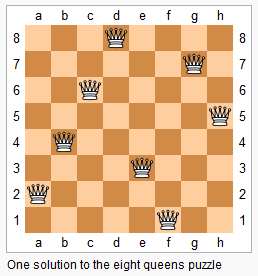
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

解法 1

class Solution {
public:
    int totalNQueens(int n) {
        vector<int> flag_col(n, 1), flag_45(2 * n - 1, 1), flag_135(2 * n - 1, 1);
        int num = 0;
        solveNQueens(flag_col, flag_45, flag_135, 0, n, num);
        return num;
    }

private:
    void solveNQueens(vector<int> &flag_col, vector<int> &flag_45, vector<int> &flag_135, int row, int n, int &nums) {
        if (row == n) {
            ++nums;
            return;
        }

        for (int col = 0; col != n; ++col)
            if (flag_col[col] && flag_45[row + col] && flag_135[n - 1 + col - row]) {
                flag_col[col] = flag_45[row + col] = flag_135[n - 1 + col - row] = 0;
                solveNQueens(flag_col, flag_45, flag_135, row + 1, n, nums);
                flag_col[col] = flag_45[row + col] = flag_135[n - 1 + col - row] = 1;
            }
    }
};

解法 2

这个解法源自 链接

核心思路如下：

1. 使用常规深度优先一层层搜索
2. 使用三个整形分别标记每一层哪些格子可以放置皇后，这三个整形分别代表列、左斜下、右斜下（col, ld, rd），二进制位为 1 代表不能放置，0 代表可以放置
3. 核心两个位运算：
   • x & -x 代表除最后一位 1 保留，其它位全部为 0
   • x & (x - 1) 代表将最后一位 1 变成 0

class Solution {
public:
    int totalNQueens(int n) {
        dfs(n, 0, 0, 0, 0);

        return this->res;
    }

    void dfs(int n, int row, int col, int ld, int rd) {
        if (row >= n) { res++; return; }

        // 将所有能放置 Q 的位置由 0 变成 1，以便进行后续的位遍历
        int bits = ~(col | ld | rd) & ((1 << n) - 1);
        while (bits > 0) {
            int pick = bits & -bits; // 注: x & -x
            dfs(n, row + 1, col | pick, (ld | pick) << 1, (rd | pick) >> 1);
            bits &= bits - 1; // 注: x & (x - 1)
        }
    }

private:
    int res = 0;
};