凌云的博客

LeetCode 算法题 62. 不同路径

分类：algorithm| 发布时间：2017-03-17 10:24:00

---

题目

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

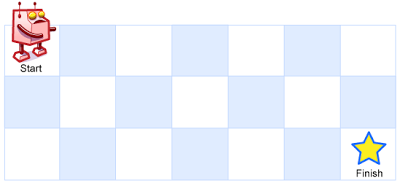
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

解法 1：递归

最简单的就是使用递归了，但是这种方法通不过测试因为耗时太长了。

class Solution {
public:
    int uniquePaths(int m, int n) {
        if (m == 1 || n == 1) return 1;
        return uniquePaths(m - 1, n) + uniquePaths(m, n -1);
    }
};

解法 2：动态规划

通过观察可以知道与起点位于同一列或同一行的格子，只有一种路径到达。 而 (i, j) 的格子的路径数为 （i - 1, j) 与 (i, j - 1) 的路径数之和。 这种思路其实跟上面的递归法是一致的，不同的是通过一个辅助的二维数组可以大量减少计算量。

class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> board(m, vector<int>(n, 1));
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                board[i][j] = board[i - 1][j] + board[i][j - 1];
            }
        }

        return board[m - 1][n - 1];
    }
};