skiplist 原理与实现

分类：algorithm| 发布时间：2019-05-08 22:52:00

概述

本文主要描述了 skiplist 的原理以及实现相关细节。

本文给出的 skiplist 的实现主要是根据 William Pugh 在论文 "Skip Lists: A Probabilistic Alternative to Balanced Trees" 所描述的算法来实现的。

skiplist 和 AVL

AVL 可用于表示如字典和有序列表等抽象数据类型。当元素以随机顺序插入时，它们工作良好。某些操作序列（例如按顺序插入元素）会产生执行效果非常差的效率。

skiplist 可能是替代 AVL 的一个不错的选择。 skiplist 通过随机数生成器来进行平衡。尽管 skiplist 可能会出现糟糕的最坏性能，但没有任何输入序列能总是导致最坏的情况发生（非常类似于随机选择枢轴元素时的快速排序）。 skiplist 不太可能是显著不平衡的（例如，对于超过 250 个元素的字典，搜索将花费超过预期时间的三倍的机会小于百万分之一）。 skiplist 具有与通过随机插入构建的 AVL 类似的平衡属性，但不要求插入是随机的。

对于许多应用来说，skiplist 比 AVL 更自然，skiplist 会使得相关的业务算法更简单。由于 skiplist 的简单性使得很容易实现一个 skiplist 算法，并且比 AVL 更快。

skiplist

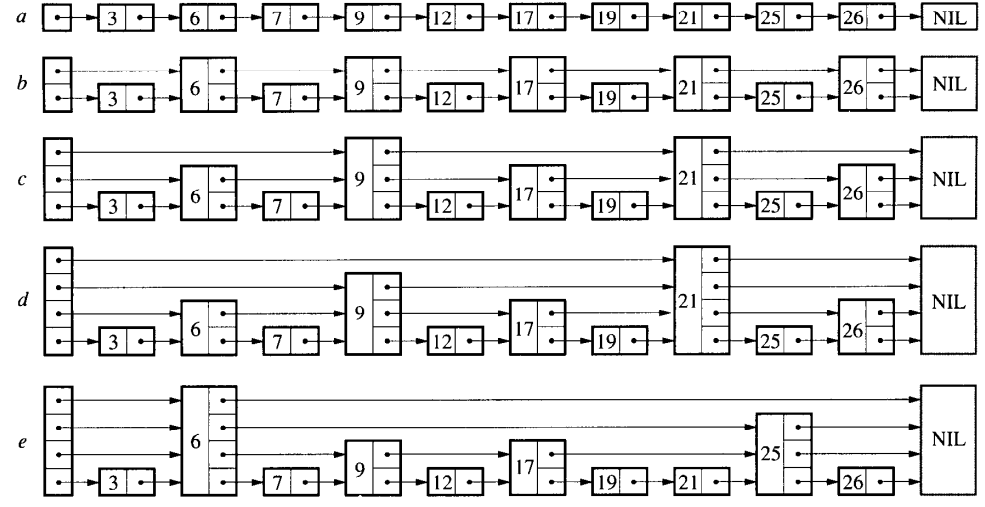
假设我们有如下图 (a) 所示的链表，当我们要搜索链表中是否存在某个值时，可能需要检查链表中的每个节点。如果我们像图 (b) 那样，链表是有序的，并且每隔一个节点有一个指向前两个节点的指针，那么在进行搜索的时候只需要检查不多于 ⌈n/2⌉+1 个节点，n 为链表的长度。如果如图 (c) 每四个节点都有一个只前四个节点的指针，我们只需要检查不多于 ⌈n/4⌉+2 个节点。如果每 2ⁱ 个节点都有一个指向前 2ⁱ 个节点的指针图 (d) 那么我们需要检查的节点可以减少到 ⌈log₂n⌉ 个。这种数据结构能用于进行快速查找，但是在进行插入和删除操作时却是不切实际的。

一个节点有 k 个前向指针时，我们称这个节点是一个 k level 的节点。如果每 2ⁱ 个节点都有一个指向前 2ⁱ 个节点的指针，那么节点的 level 分布将是一个简单的模式： 50% 的节点 level 值为 1，25% 的节点 level 值为 2，12.5% 的节点 level 值为 3 等等。当我们为每个节点按照概率随机地选择一个 level 时情况会怎样呢？如图 (e)。这种情况下删除或者插入节点只需要修改局部的少数指针，其他已在链表中的节点 level 不变。由于这种数据结构是在链表的基础上添加指针用于跳过链表的某些节点，因此这种数据结构称为跳表（skiplist）。

skiplist 算法

下面，我们通过一个用 Python 实现的 skiplist 为例，讲解 skiplist 实现过程中的几个关键点。

首先我们定义下 skiplist 中的节点：

class Node(object):
    def __init__(self, level, key, value):
        self.forward = [None] * level
        self.key = key
        self.value = value

其中 forward 是一个数组，包含了 n 个前向指针，数组的长度表示此节点的 level 值。
key 用于对链表中的节点进行排序
value 保存了节点的值，由于是 Python 实现的，value 可以保存任意类型的值

初始化

在对 skiplist 进行初始化时需要指定 skiplist 的 level 值的最大值，以及各个 level 的节点的概率分布。

class Skiplist(object):
    def __init__(self, max_level = 32, p = 0.5):
        self.max_level = max_level
        self.header = Node(max_level, 0, 0)
        self.current_level = 0
        self.__probability = p

搜索

class Skiplist(object):
    def search(self, key):
        x = self.header
        for level in range(self.current_level - 1, -1, -1):
            while x.forward[level] is not None and x.forward[level].key < key:
                x = x.forward[level]

        x = x.forward[0]
        if x is not None and x.key == key:
            return x.value
        else:
            return None

在进行搜索时，我们总是从 skiplist 当前的 level 开始往前跳（尽可能的跳过更多的点以减少要检查的点）。当发现当前层的前向节点的 key 值比要搜索的 key 要大时表示如果往前跳有可能会跳过目标节点，此时需要进行 level 的下探，直到 level 为 1 的层（Python 的数组是 zero-base 的，因此对应了代码中的 0）。

插入

插入代码如下：

class Skiplist(object):
    def insert(self, key, value):
        update = [None] * self.max_level
        x = self.header
        for level in range(self.current_level - 1, -1, -1):
            while x.forward[level] is not None and x.forward[level].key < key:
                x = x.forward[level]

            update[level] = x

        x = x.forward[0]
        if x is not None and x.key == key:
            # found key, just update value
            x.value = value
        else:
            new_level = self.__random_level()
            if new_level > self.current_level:
                for level in range(self.current_level, new_level):
                    update[level] = self.header

                self.current_level = new_level

            x = Node(new_level, key, value)
            for level in range(0, new_level):
                x.forward[level] = update[level].forward[level]
                update[level].forward[level] = x

前面部分类似 search 算法，查找要插入的节点的 key 是否已经存在，若存在则更新已有的节点的值，否则进行节点插入。在新建节点的时候使用了随机的方法决定当前节点的 level 值。

删除

class Skiplist(object):
    def delete(self, key):
        update = [None] * self.max_level
        x = self.header
        for level in range(self.current_level - 1, -1, -1):
            while x.forward[level] is not None and x.forward[level].key < key:
                x = x.forward[level]

            update[level] = x

        x = x.forward[0]
        if x is not None and x.key == key:
            for level in range(0, self.current_level):
                if update[level].forward[level] != x:
                    break

                update[level].forward[level] = x.forward[level]

            del x
            while self.current_level > 0 and\
                    self.header.forward[self.current_level - 1] == None:
                self.current_level -= 1

删除节点时会使用类似 search 的算法找出要删除的节点，然后更新所有指向此节点的前向节点。

随机选择节点的 level

class Skiplist(object):
    def __random_level(self):
        new_level = 1
        while random.random() < self.__probability:
            new_level += 1

        return min(self.max_level, new_level)

在初始化 skiplist 的时候，我们提到了需要指定 skiplist 的 max_level，以及各个 level 的分布概率。其中我们通过 random_level 里的算法保证了节点的 level 的概率分布是大致符合我们的预期的。

max_level 应该怎么选呢？这取决于我们选定的 p 值以及预期 skiplist 最多会容纳多少个节点，比如 p 为 1/2， skiplist 最多容纳 2^16 个节点，则可以将 max_level 设置为 16。

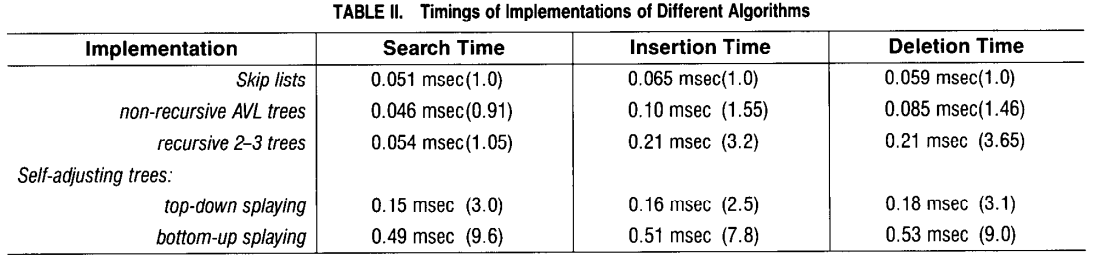
性能对比

这里我直接贴出了论文中作者做的不同算法的耗时对比。虽然这个对比是很多年前做的了，其耗时的绝对时间已经没有参考价值了，但是其相对耗时还是有一定参考价值的。

总结

skiplist 和 AVL 有着类似的性能表现，但 skiplist 实现简单，逻辑直观
由于 skiplist 使用了随机算法来决定节点的 level，因此没有哪种插入顺序能总是导致 skiplist 出现最差性能
skiplist 这是文中的 skiplist 的完整代码

凌云的博客

行胜于言